在我读研究生第一年,我对于数学有了一次顿悟,这改变了我对整个机器学习领域的看法与思路。当时我选择研究的方向是机器学习。这是一个交叉学科的领域,结合了计算机科学、统计学和其他很多的数学学科,比如优化方法和线性代数。需要学的内容非常多,所有的研一的学生都在努力地消化吸收这些海量的概念。
一天晚上,我坐在办公室里试图去对线性代数有所悟。虽然我有一本很好的教材—基尔伯特·斯特朗所著的《线性代数入门》—作为我的引导,但我一直没办法取得进展。我看着各种各样的定义,特征分解、乔丹正规型、矩阵翻转等等,就在想:“为什么?为什么这些都看着那么诡异?为什么翻转要这么定义?真正地仔细想想,为什么所有这些矩阵运算都用现在这个方式来定义?”
就在我无望地盯着满屏的数学符号的时候,突然脑海里一道灵光闪现。我意识到:数学是一种设计!在此之前,我一直把数学当成一种宇宙真理一样的学习。它完美超然、且几乎凡人所不可知。但在那夜之后,我意识到数学也仅仅是一个人类创建的工具。数学是被设计出来的,就像软件编程是被设计出来的一样,也使用了很多类似的设计原理。这些原理也许不那么明显,但都是可以被理解的。从那个时刻起,对我而言数学从不可知变为合理
数学是由对象、运算以及一些简化形式构成的系统。它被设计来对真实世界的现象进行建模。与所有的设计类似,它也有一定的自由度。这一系统可以这样设计,当然也可以那样设计。一个矩阵在极坐标体系里可以被设计为一个圆球。只要运算是一致的,这种设计就没有关系;它仅仅就是一个简化的缩写。在某个时间点,某个人制定了这些设计。他们挑选了这些对象与运算方式,并指定了组织在一起的规则。如果设计得比较好,那么基于这些基本的决定,很多有用的、可被证明的特性就出现了。这整套系统就可以被用来对我们所处于的这个世界进行建模:比如抛物在空间里的运行方式,声波穿过以太的方式,或者股票价格的涨跌。现实世界包含了层层堆叠的复杂性。设计良好的数学系统则给出了干净简洁的工具来表征每一层的现实世界。
线性代数被设计来表征线性方程体系。而线性方程则被设计来表征线性关系,即一个对象被写成其他对象相乘的和的关系。在线性代数的缩写里,一个线性关系被表征为一个线性算子,即一个矩阵。线性算子被设计得很简单,因此他们的效应就可以被完全的分析。线性算子可以做两件事:旋转和增缩。这里,在几何与代数的交界处,一些神奇的事情发生了。代数里的乘和加运算被转化成了向量空间里的向量的旋转和增缩。这样就可以让我们用代数的方法来分析线性算子的几何效应,即把矩阵分解成它的组成部分:需要旋转多少、需要扩展或是压缩多少以及在哪个方向上进行。
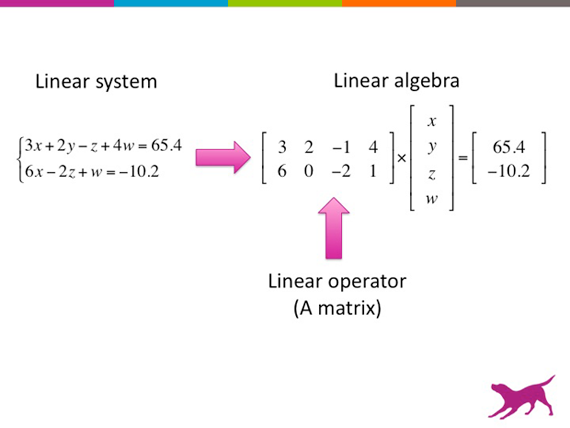
来源:Alice Zheng授权使用
数学所包含的某些设计原则也展现在软件工程里面。以抽象代数为例,抽象代数本质上就是一个对象层级设计的实践。它的目的是用近可能少的原料,并一次加入一个或几个原料,来查看会得到什么有趣和有用的产出。一个“群”被定义成一些元素与一个运算的集合(运算必须要满足一定的条件来保证它的行为不会太奇怪)。一个“环”则是一种特殊的群,它具有两种可以被泛化成加与乘的运算。一个“域”则是一种特殊的环,它具有四种运算(可以被泛化成加、减、乘、除)。这种定义立刻就听着像是软件工程里的概念:这是一个对象的层级结构,“域”继承自“环”,而“环”则继承自“群”!
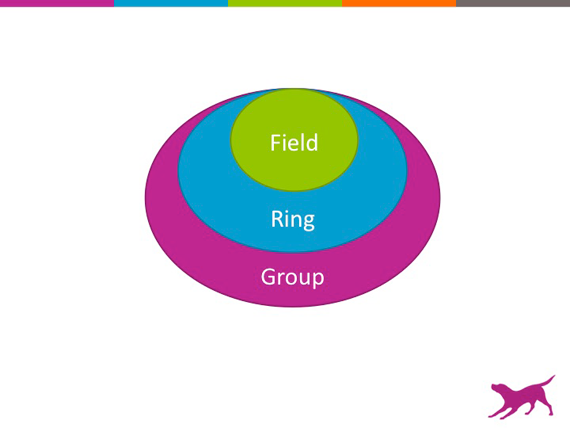
来源:Alice Zheng授权使用
现在让我们看看实数系统。这是另外一个层级化对象设计的例子,但细节上有一些有趣的变化。让我们从自然数开始。其实自然数就是我们用手指头数数的扩展。接着,让我们以零点为中心加入自然数的镜像——负数。这样我们就获得了整数的概念。再把整数结合上加法和乘法运算,我们就得到了一个上面所说的“环”。如果再结合上乘法和除法,我们就生成了有理数,也就是得到了一个“域”。如果故事就此为止,我们会有一个不错的结果:我们有一堆数和一些运算。对这些数运用我们的运算,我们还是会得到同样类型的数。好耶!但不幸的是,我们的几何学家邻居会来敲门,并问:“圆形的面积是什么样的数?直角三角形的斜边长度是什么数?”这些数看起来并不是某两个整数的比例值。
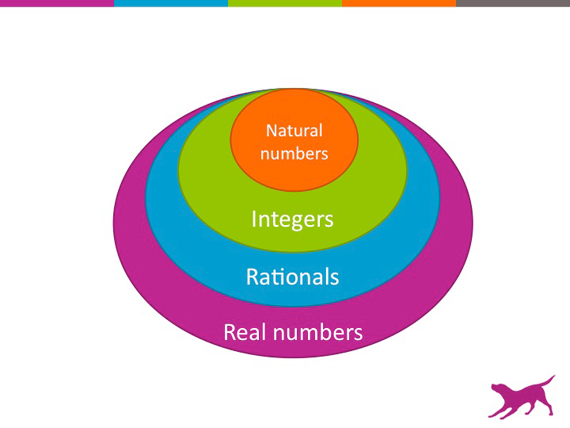
来源:Alice Zheng授权使用
上述的这些发现打开了无理数的泄洪闸,搅乱了我们设计的干净整齐的数的系统。有理数和无理数都是有用的数,因此最好能有一个表达方式来统一处理两者。但是,源于那个烦人的“无穷”的概念,这两种数是如此的不同。无理数是无限长的,因此很不容易处理;而有理数是有顺序的,且可数的;无理数是无法数的。我们整整花了几千年来找到一个解决方法去统一处理有理数和无理数。现在最佳的提议是用有限小数方式表示:每个实数都可以被认为是无穷数列的等价类。整个数的系统的结构都是层级化的,而且大部分的元素实际上都没办法被有穷图灵机计算。到头来,我们可说实数其实完全不“真实”存在,它们都是被构造出来的。
上述这些只是实际在用的数学设计的一小部分例子。我们的文化在灌输一个很奇怪的理念,即数学是很难的,数学看起来是太抽象、太难学、太难理解,所以几乎无法学会。但换个角度来看,数学和软件工程有着令人惊讶的相似性。这两个学科都会使用自己的行话与表示法。但一旦我们理解了这些行话后,我们就可以看到数学的灵与肉了。理解数学的设计原则可以引领我们进入这个充满层级对象和变换表现的世界。在对于数学有更多的了解后,就可能帮助我们产生更多的数学与软件工程学交叉的想法。甚至我们也能开始去对数学的设计做修改,产生新的数学设计。想想,现在的实数系统已经非常得古老和笨拙了。是时候来点新的东西了!





